C++ 中文周刊 第34期
从reddit/hackernews/lobsters/meetingcpp摘抄一些c++动态
每周更新
| 周刊项目地址|在线地址 |知乎专栏 | 腾讯云+社区 |
欢迎投稿,推荐或自荐文章/软件/资源等,请提交 issue
资讯
编译器信息最新动态推荐关注hellogcc公众号
文章
double转int怎么搞?
bool to_int64_simple(double x, int64_t *out) {
int64_t tmp = int64_t(x);
*out = tmp;
return tmp == x;
}
这个有UB的,不能这么写,bit_cast可以用
或者union
typedef union {
struct {
uint64_t fraction : 52;
uint32_t exp_bias : 11;
uint32_t sign : 1;
} fields;
double value;
} binary64_float;
bool to_int64(double x, int64_t *out) {
binary64_float number = {.value = x};
const int shift = number.fields.exp_bias - 1023 - 52;
if (shift > 0) {
return false;
}
if (shift <= -64) {
if (x == 0) {
*out = 0;
return true;
}
return false;
}
uint64_t integer = number.fields.fraction | 0x10000000000000;
if (integer << (64 + shift)) {
return false;
}
integer >>= -shift;
*out = (number.fields.sign) ? -integer : integer;
return true;
}
作者做了个压测,比较哪个快。我觉得有UB就别比较了。没啥意义
类似optional,但是
C++ 中的
std::optional在 C++17 中才引入,并且让std::optional支持monadic operations的提案要在 C++23 才引入。OneFlow 用自己的方式实现了Maybe。
其实就是要optional支持更多的链式动作,比如add_then or_else之类的,更函数式一点
社区有一个实现 有这些功能
比较三个编译器,一个简单的find,作者发现ICC比其他两个要快?为什么
// Returns the index of the first occurrence of k in the n integers
// pointed by v, or n if k is not in v.
//优化效果相同
size_t find_int_c(int k, const int* v, size_t n)
{
for (size_t i = 0; i != n; ++i)
if (v[i] == k)
return i; return n;
}
// Returns the index of the first occurrence of k in the n integers
// pointed by v, or n if k is not in v.
//优化效果不同,icc更快,都比c版要快
size_t find_int_cpp(int k, const int* v, size_t n)
{
return std::find(v, v + n, k) — v;
}
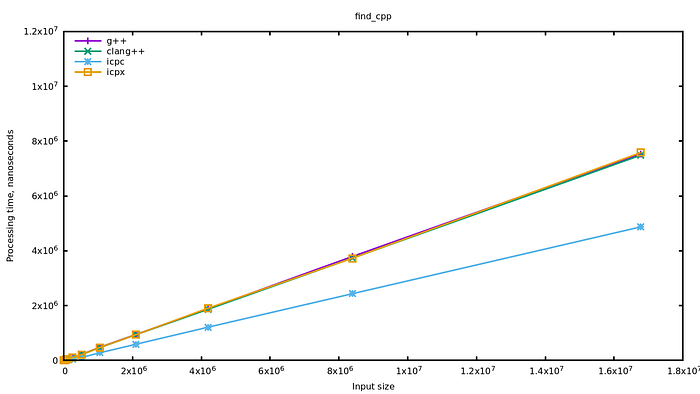
作者简单猜测优化策略,手写了个循环展开版本的find 优化效果相同,但还是没有icc的find快
// Returns the index of the first occurrence of k in the n integers
// pointed by v, or n if k is not in v.
size_t find_int_c_unrolled_8(int k, const int* v, size_t n)
{
size_t i = 0; for (; n - i >= 8; i += 8)
{
if (v[i] == k)
return i;
if (v[i + 1] == k)
return i + 1;
if (v[i + 2] == k)
return i + 2;
if (v[i + 3] == k)
return i + 3;
if (v[i + 4] == k)
return i + 4;
if (v[i + 5] == k)
return i + 5;
if (v[i + 6] == k)
return i + 6;
if (v[i + 7] == k)
return i + 7;
} for (; i != n; ++i)
if (v[i] == k)
return i; return n;
}
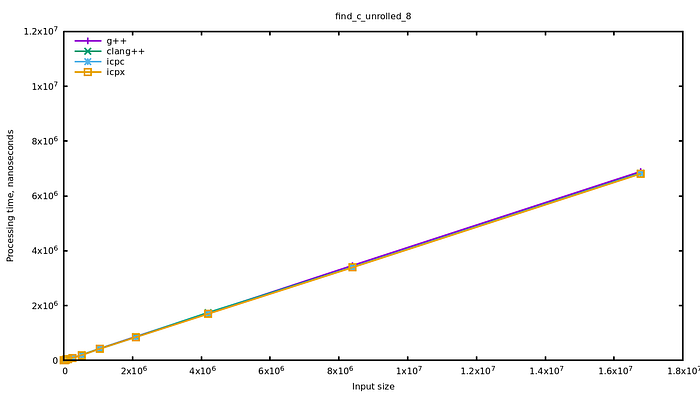
那为什么icc的find更快?用了simd?
手写了一版simd的find,再进行比较
// Returns the index of the first occurrence of k in the n integers
// pointed by v, or n if k is not in v.
size_t find_int_sse2(int k, const int* v, size_t n)
{
// We are going to check the integers from v four by four. // This instruction copies the searched value k in each of the
// four 32-bits lanes of the 128 bits register. If k…k represents
// the 32 bits of k, the register then looks like this:
//
// [ k…k | k…k | k…k | k…k ]
//
const __m128i needle = _mm_set1_epi32(k); // Here we just reinterpret the pointer v as a pointer to 128 bits
// vectors. This will allow to access the integers four by four.
// And yes, I do use a C cast like a barbarian.
const __m128i* p = (const __m128i*)v; // A division! Will the compiler emit a shift for it?
const size_t iterations = n / 4;
const size_t tail = n % 4; for (size_t i(0); i != iterations; ++i, ++p)
{
const __m128i haystack = *p; // This compares all four 32 bits values of needle (so four
// times the searched value) with four integers pointed by p,
// all at once. All bits of a 32 bits lane are set to 1 if the
// values are equal. The operation looks like this:
//
// [ k…k | k…k | k…k | k…k ]
// cmpeq [ a…a | b…b | k…k | c…c ]
// = [ 0…0 | 0…0 | 1…1 | 0…0 ]
//
const __m128i mask = _mm_cmpeq_epi32(needle, haystack); // We cannot compare mask against zero directly but we have an
// instruction to help us check the bits in mask. // This instruction takes the most significant bit of each of
// the sixteen 8 bits lanes from a 128 bits register and put
// them in the low bits of a 32 bits integer.
//
// Consequently, since there are four 8-bits lanes in an
// integer, if k has been found in haystack we should have a
// 0b1111 in eq. Otherwise eq will be zero. For example:
//
// movemask [ 0…0 | 0…0 | 1…1 | 0…0 ]
// = 0000 0000 0000 0000 0000 0000 1111 0000
//
const uint32_t eq = _mm_movemask_epi8(mask); // Since we are back with a scalar value, we can test it
// directly.
if (eq == 0)
continue; // Now we just have to find the offset of the lowest bit set
// to 1. My laptop does not support the tzcnt instruction so I
// use the GCC builtin equivalent.
const unsigned zero_bits_count = __builtin_ctz(eq); // Each 4 bits group in eq matches a 32 bits value from mask,
// thus we divide by 4.
return i * 4 + zero_bits_count / 4;
} // Handle the last entries if the number of entries was not a
// multiple of four.
for (size_t i(iterations * 4); i != n; ++i)
if (v[i] == k)
return i; return n;
}
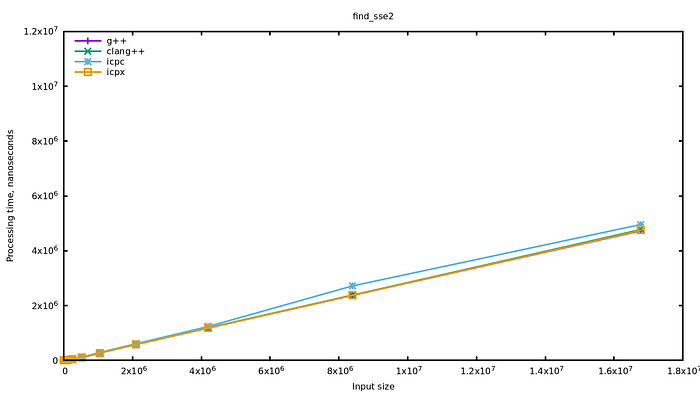
基本可以证实ICC用了simd优化的find了,实现看不到
代码以及测试数据在这里
逐个介绍-ffast-math优化都是什么
-ffinite-math-only and -fno-signed-zeros
这两个优化直接干掉NAN/inf -0.0场景 x+0.0一定会被优化成x,x-x一定被优化成0 x*0.0 一定被优化成0.0
干掉NaN inf -0.0的影响
但是,如果遇到NaN Inf -0.0判断,不能保证条件是true/false
-fno-trapping-math
浮点数可能有异常的,触发SIGFPE信号,溢出FE_OVERFLOW,生成NaN之类的
// Compile as "gcc example.c -D_GNU_SOURCE -O2 -lm"
#include <stdio.h>
#include <fenv.h>
void compute(void) {
float f = 2.0;
for (int i = 0; i < 7; ++i) {
f = f * f;
printf("%d: f = %f\n", i, f);
}
}
int main(void) {
compute();
printf("\nWith overflow exceptions:\n");
feenableexcept(FE_OVERFLOW);
compute();
return 0;
}
再比如,除0.0
double arr[1024];
void foo(int n, double x, double y) {
for (int i = 0; i < n; ++i) {
if (arr[i] > 0.0)
arr[i] = x / y;
}
}
编译器会加上处理异常的代码段。开了这个flag就可以直接干掉
-fassociative-math
各种交换律结合律优化
float a[1024];
float foo(void) {
float sum = 0.0f;
for (int i = 0; i < 1024; ++i) {
sum += a[i];
}
return sum;
}
优化成
float a[1024];
float foo(void) {
float sum0 = sum1 = sum2 = sum3 = 0.0f;
for (int i = 0; i < 1024; i += 4) {
sum0 += a[i ];
sum1 += a[i + 1];
sum2 += a[i + 2];
sum3 += a[i + 3];
}
return sum0 + sum1 + sum2 + sum3;
}
-fno-math-errno
全局errno设置,这个会影响性能
比如
double foo(double x) {
return sqrt(x);
}
默认会判断x,走两个逻辑
foo:
pxor xmm1, xmm1
ucomisd xmm1, xmm0
ja .L10
sqrtsd xmm0, xmm0
ret
.L10:
jmp sqrt
开了这个优化直接走sqrtsd
foo:
sqrtsd xmm0, xmm0
ret
不过这个优化会导致一个问题,malloc的errno设置也被优化掉了,默认认为malloc错误也不设置errno,这有个bug 88576. 目前还没修
看这个比较 能看到开启开关直接perror被优化掉了
-freciprocal-math
x/y 优化成 x*(1/y),因为乘比除快
-funsafe-math-optimizations
还是各种算式简化
| 原来的 | 优化后 |
|---|---|
sqrt(x)*sqrt(x) |
x |
sqrt(x)*sqrt(y) |
sqrt(x*y) |
exp(x)*exp(y) |
exp(x+y) |
x/exp(y) |
x*exp(-y) |
x*pow(x,c) |
pow(x,c+1) |
pow(x,0.5) |
sqrt(x) |
(int)log(d) |
ilog(d) |
sin(x)/cos(x) |
tan(x) |
-fcx-limited-range
(a + ib) \times (c + id) = (ac - bd) + i(bc + ad)
\frac{a + ib}{c + id} = \frac{ac + bd}{c^2 + d^2} + i\frac{bc - ad}{c^2 + d^2}
用这两个算式来优化乘除,规避NaN
以前头文件都适用宏,但是2021年了,大家都用pragma once了
#ifndef HEADER_FOOBAR
#define HEADER_FOOBAR
class FooBar
{
// ...
};
#endif // HEADER_FOOBAR
#pragma once
以后普及了module就再也不用这些东西了,当前#pragma once是最优雅的,主流编译器都实现了
这个上一期漏了,主要是介绍实现基于range的projection遇到的困难
实现了几种LRUcache,没啥说的,看代码
参数丢失信息,比如
run< true, false >();
乍一看看不懂true false是啥意思
怎么办?用enum表达bool的语义, godbolt
#include <iostream>
enum class ShouldAddFoo : bool {};
enum class ShouldAddBar : bool {};
// C++17
// template
// <
// typename Enum,
// typename std::enable_if_t
// <
// std::is_same_v< std::underlying_type_t< Enum >, bool >
// >* = nullptr
// >
// constexpr bool operator*( Enum const value )
// {
// return static_cast< bool >( value );
// }
// C++20
template< typename Enum >
concept BoolEnum = std::is_enum_v< Enum >
&& std::is_same_v< std::underlying_type_t< Enum >, bool >;
constexpr bool operator*( BoolEnum auto const value )
{
return static_cast< bool >( value );
}
template< ShouldAddFoo addFoo, ShouldAddBar addBar >
void run()
{
if constexpr ( *addFoo ) { std::puts( "addFoo" ); }
if constexpr ( *addBar ) { std::puts( "addBar" ); }
}
int main()
{
run< ShouldAddFoo{ true } , ShouldAddBar{ false } >();
run< ShouldAddFoo{ false } , ShouldAddBar{ true } >();
// run< ShouldAddBar{ false } , ShouldAddFoo{ true } >(); // compile-time error
return 0;
}
一个简单场景
int foo(int n);
int test(int const& n)
{
auto sum = 0;
sum += foo(n);
sum += foo(n);
return sum;
}
如果foo和test同属一个TU/foo是inline的,test中的foo能被优化掉
如果不属于同一个TU,可能LTO能优化到
当然,也可以用__attribute__((noinline)) 强制不优化
即使不在同一个TU,也可以优化的到
比如 __attribute__((const)) __attribute__((pure)).
另外如果是循环场景,即使不是inline,编译器也能从其他优化角度来优化,比如 value numbering, common subexpression elimination, loop-invariant code motion
TODO: 这个我这边打不开 SSL_ERROR_RX_RECORD_TOO_LONG
没啥说的,看你需不需要value
delete表达的含义过于精确,如果你单纯的不想某些函数被调用,不实现它和delete它效果是类似的,delete用在特定的重载上更有说服力
比如
struct MoveOnly {
MoveOnly(MoveOnly&&);
MoveOnly& operator=(MoveOnly&&);
MoveOnly(const MoveOnly&) = delete; // 不实现它也一样
MoveOnly& operator=(const MoveOnly&) = delete; // 不实现它也一样
};
再比如
template<class T>
auto cref(const T&) -> std::reference_wrapper<const T>;
int i = 42;
auto r1 = std::cref(i); // OK
auto r2 = std::cref(42); // OK but dangling!
42这种场景不应该通过编译,对应的函数被默认实现了,所以要delete
template<class T>
auto cref(const T&) -> std::reference_wrapper<const T>;
template<class T>
auto cref(const T&&) = delete;
auto r2 = std::cref(42); // Error, best match is deleted
展望了一下Continuation Monad 和std::execution以及协程的结合,仅仅是展望。这东西是函数式编程语言的基本概念。但是对于c/c++程序员没有普及开来。在迎接std::execution普及之前,最好简单了解一下(随便看一个haskell教程学习一番)
这是c#的。编译器的inline不够好,还手动调整了一番让编译器更好的inline
介绍一个UB啊
int C = 1;
int c_cpp = C/C++;
经典求值顺序问题,用clang会给你警告
warning: unsequenced modification and access to 'C' [-Wunsequenced]
这玩意在中国的版本是 i++ + i++之类的
介绍一个经典问题,如何同一个函数 返回值类型不同?一个wrapper类封装类型
#include <iostream>
#include <typeinfo>
template <typename T, typename T2> // primary template (1)
struct ReturnType;
template <> // full specialization for double, double
struct ReturnType <double, double> {
typedef double Type;
};
template <> // full specialization for double, bool
struct ReturnType <double, bool> {
typedef double Type; // (2)
};
template <> // full specialization for bool, double
struct ReturnType <bool, double> {
typedef double Type;
};
template <> // full specialization for bool, bool
struct ReturnType <bool, bool> {
typedef int Type;
};
template <typename T, typename T2>
typename ReturnType<T, T2>::Type sum(T t, T2 t2) { // (3)
return t + t2;
}
int main() {
std::cout << "typeid(sum(5.5, 5.5)).name(): " << typeid(sum(5.5, 5.5)).name() << '\n';
std::cout << "typeid(sum(5.5, true)).name(): " << typeid(sum(5.5, true)).name() << '\n';
std::cout << "typeid(sum(true, 5.5)).name(): " << typeid(sum(true, 5.5)).name() << '\n';
std::cout << "typeid(sum(true, false)).name(): " << typeid(sum(true, false)).name() << '\n';
}
比较猥琐的需求
介绍stl reduce操作相关函数
#include <iostream>
#include <numeric>
#include <string>
#include <vector>
#include <execution>
int main()
{
std::vector nums {32,16,8, 4, 2, 1};
std::cout << std::accumulate(nums.begin()+1, nums.end(), *nums.begin(), std::minus<>{}) <<'\n';
std::cout << std::reduce(nums.begin()+1, nums.end(),*nums.begin(), std::minus<>{}) <<'\n';
std::cout << std::reduce(std::execution::seq, nums.begin()+1, nums.end(),*nums.begin(), std::minus<>{}) <<'\n';
std::cout << std::reduce(std::execution::unseq, nums.begin()+1, nums.end(),*nums.begin(), std::minus<>{}) <<'\n';
std::cout << "======\n";
std::cout << std::reduce(std::execution::par, nums.begin()+1, nums.end(),*nums.begin(), [](int a, int b){
std::cout << a << " " << b << '\n';
return a-b;
}) <<'\n';
}
/*
1
25
25
1
======
16 8
4 2
8 2
32 6
26 1
25
*/
注意accumulate严格右折叠,但reduce不保证这个顺序
transform_reduce用法不太一样
作者在开发他的lex库,处理报错的时候遇到了方案抉择
视频
- [MUC++] Matt Godbolt - Cool Compiler Tidbits compile explore作者手把手教你学汇编
cppcon 2021越来越近了,下期回顾下cppcon 2020 的视频
项目
- imgui 是个非常轻量的GUI库,发布1.85版本,修复一些bug
- replxx 一个cli库,发布了0.04版本
- 一个static vector实现 cppcon也会有这个实现的讨论,后面视频放出来展开讲一下
- json 3.10.4版本发布,修复一些bug,废弃一些接口
