C++ 中文周刊第15期

从reddit/hackernews/lobsters/meetingcpp摘抄一些c++动态。

每周更新

周刊项目地址 github，在线地址｜知乎专栏

欢迎投稿，推荐或自荐文章/软件/资源等，请提交 issue

资讯

编译器信息最新动态推荐关注hellogcc公众号

本周周报github直达

文章

Daniel Lemire 整的新活，如何更快的计算一个数有几位，正常的算法就是除10

从数学角度就是取十的对数，这里考虑二进制，log₁₀(X) = log₂(X) / log₂(10) 首先，不能用除，效率低，考虑乘和位移

log₂(X)简单

int int_log2(uint32_t x) { return 31 - __builtin_clz(x|1); }

然后考虑 log₂(10) 简单估算是乘9除32 除以32可以改成位移

    static uint32_t table[] = {9, 99, 999, 9999, 99999, 
    999999, 9999999, 99999999, 999999999};
    int y = (9 * int_log2(x)) >> 5;
    y += x > table[y];
    return y + 1;

luajit用到了类似的技巧这里比乘9除32更精密一些

/* min(2^32-1, 10^e-1) for e in range 0 through 10 */
static uint32_t ndigits_dec_threshold[] = {
  0, 9U, 99U, 999U, 9999U, 99999U, 999999U,
  9999999U, 99999999U, 999999999U, 0xffffffffU
};

/* Compute the number of digits in the decimal representation of x. */
static MSize ndigits_dec(uint32_t x)
{
  MSize t = ((lj_fls(x | 1) * 77) >> 8) + 1; /* 2^8/77 is roughly log2(10) */
  return t + (x > ndigits_dec_threshold[t]);
}

更进一步,ceil(log10(2j)) * 232 + 232 – 10ceil(log10(2j)) 考虑这种算法，生成的table又省了一些

int fast_digit_count(uint32_t x) {
  static uint64_t table[] = {
      4294967296,  8589934582,  8589934582,  8589934582,  12884901788,
      12884901788, 12884901788, 17179868184, 17179868184, 17179868184,
      21474826480, 21474826480, 21474826480, 21474826480, 25769703776,
      25769703776, 25769703776, 30063771072, 30063771072, 30063771072,
      34349738368, 34349738368, 34349738368, 34349738368, 38554705664,
      38554705664, 38554705664, 41949672960, 41949672960, 41949672960,
      42949672960, 42949672960};
  return (x + table[int_log2(x)]) >> 32;
}

table的数用脚本找的

最后，给个benchmark

这三个版本明显第三个要快一些

Different ways to achieve SFINAE

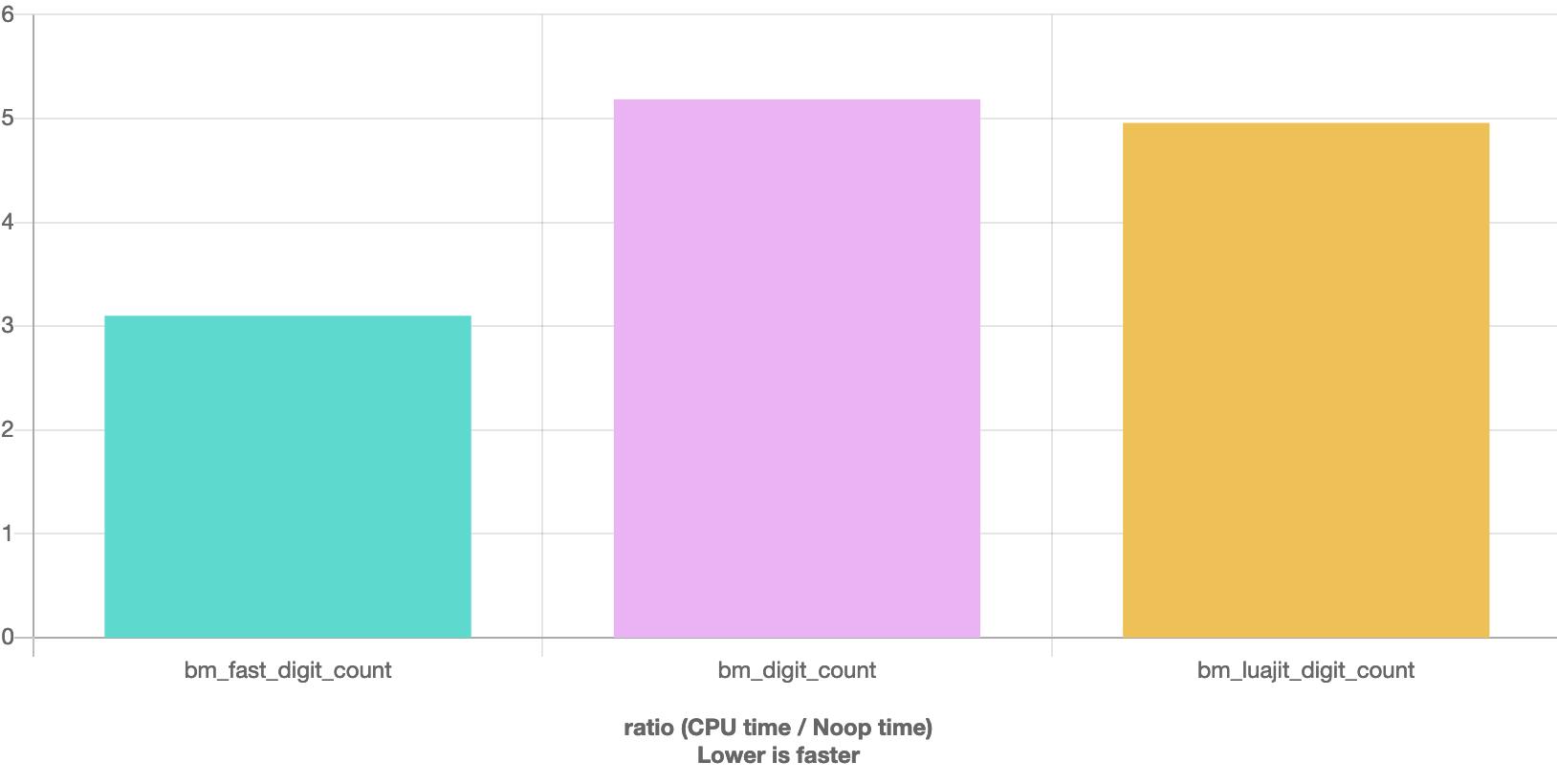
回顾SFINAE的几种写法,匹配失败不是错误，核心是匹配

基本写法

#include <iostream>

class MyType {
public:
    using type = char;
};

class MyOtherType {
public:
    using other_type = int;
};

template<typename T>
void foo(T bar, typename T::type baz)
{
    std::cout << "void foo(T bar, typename T::type baz) is called\n";
}

template<typename T>
void foo(T bar, typename T::other_type baz)
{
    std::cout << "void foo(T bar, typename T::other_type baz) is called\n";
}


int main()
{
    MyType m;
    MyOtherType mo;
    foo(m, 'a');
    foo(mo, 42);
    // error: no matching function for call to 'foo(MyOtherType&, const char [3])'
    // foo(mo, "42");
}
/*
void foo(T bar, typename T::type baz) is called
void foo(T bar, typename T::other_type baz) is called
*/

decltype std::declval

#include <iostream>

class MyType {
public:
    using type = char;
};

class MyOtherType {
public:
    using other_type = int;
};

template<typename T>
decltype(typename T::type(), void()) foo(T bar)
{
    std::cout << "decltype(typename T::type(), void()) foo(T bar) is called\n";
}

template<typename T>
decltype(typename T::other_type(), void()) foo(T bar)
{
    std::cout << "decltype(typename T::other_type(), void()) is called\n";
}


int main()
{
    MyType m;
    MyOtherType mo;
    foo(m);
    foo(mo);
    // error: no matching function for call to 'foo(MyOtherType&, const char [3])'
    // foo(mo, "42");
}

经典enable_if

template<typename T>
std::enable_if_t<std::is_integral<T>::value, T> f(T t){
    //integral version
}
template<typename T>
std::enable_if_t<std::is_floating_point<T>::value, T> f(T t){
    //floating point version
}

concept

#include <concepts>

template<typename T>
class MyClass {
public:
  void f(T x) {
    std::cout << "generic\n"; 
  }
  
  void f(T x) requires std::floating_point<T> {
    std::cout << "with enable_if\n"; 
  }
};

c++ tip of week 228 Did you know that C++ allows accessing private members with friend injection

比较经典的技巧了。

class foo {
 private:
  int data;
};

template<int foo::*Ptr>
int& get_data(foo& f) {
  return f.*Ptr;
}

template<int foo::*Ptr>
struct foo_access {
  friend int& get_data(foo& f) {
    return f.*Ptr;
  }
};

template struct foo_access<&foo::data>;
int& get_data(foo&);

int main() {
  foo f{};
  get_data(f) = 42; // access private data member
}

Compile-time pre-calculations in C++

得益于constexpr/consteval 可以编译时求质数。给了两种求质数的方法

一种常规

// \file compile-time-cpp/is-prime-17-constexpr-func.cc
#include <iostream>
  
constexpr bool is_prime(int v) {
  for (int i = 2; i < v; i++) {
    if (v % i == 0) {
      return false;
    }
  }
  return true;
}
  
template<int v>
struct IsPrime {
  static constexpr bool value = is_prime(v);
};
  
int main() {
  std::cout << 7 << " : " << IsPrime<7>::value << std::endl;
  std::cout << 2000 << " : " << IsPrime<2000>::value << std::endl;
  std::cout << 2003 << " : " << IsPrime<2003>::value << std::endl;
  
  return 0;
}

一种是生成一个数组

#include <iostream>
#include <array>
  
template<int v>
consteval std::array<int, v + 1> sieve() {
  std::array<int, v + 1> arr = {};
  for(long long i = 2; i <= v; i++) {
    if(arr[i]) {
      continue;
    }
    for(long long j = i * i; j <= v; j+= i) {
      arr[j] = 1;
    }
  }
  return arr;
}
  
int main() {
  auto sieve_array = sieve<12345>();
  std::cout << 7 << " : " << sieve_array[7] << std::endl;
  std::cout << 2000 << " : " << sieve_array[2000]<< std::endl;
  std::cout << 2003 << " : " << sieve_array[2003]<< std::endl;
  
  size_t i = 0;
  std::cin >> i;
  std::cout << sieve_array[i] << std::endl;
  
  return 0;
}

Compilation speed humps: [std::tuple](https://en.cppreference.com/w/cpp/utility/tuple)

讨论了几种降低tuple编译时间的方法, 主要源头type_element，替代方案，自己实现type_list或者用type_pack_element

#ifdef __has_builtin
    #if __has_builtin(__type_pack_element)
        #define MZ_HAS_TYPE_PACK_ELEMENT
    #endif
#endif

#ifdef MZ_HAS_TYPE_PACK_ELEMENT

template <typename... T, size_t N>
struct type_list_selector<type_list<T...>, N>
{
    using type = __type_pack_element<N, T...>;
};

#else

// ... all the previous type_list_selectors ...

#endif

Smarter C/C++ inlining with __attribute__((flatten))

小函数inline，但是在组合的函数里，函数的冷热程度不同，可能导致多余的inline

__attribute__((always_inline)) inline void do_thing(int input)
{
    // this code is always inlined at the call site
}

void hot_code()
{
    // the program spends >80% of its runtime in this function
    while (condition) {
        ...
        do_thing(y);
        ...
    }
}
void cool_code()
{
    // the program spends <5% of its runtime in this function
    ...
    do_thing(a);
    do_thing(b);
    do_thing(c);
}

引入__attribute__((flatten)) 让上层来决定内部小函数inline

void do_thing(int input)
{
    // this code is not always inlined at the call site
}

__attribute__((flatten)) void hot_code()
{
    // the program spends >80% of its runtime in this function
    while (condition) {
        call_something();   // inlined!
        do_thing(y);        // inlined!
        other_thing();      // also inlined!
    }
}

void cool_code()
{
    // the program spends <5% of its runtime in this function
    ...
    do_thing(a);            // not inlined!
    do_thing(b);            // not inlined!
    do_thing(c);            // guess!
}

非常好用

Design issues in LLVM IR

TODO: 看不懂

视频

C++ Weekly - Ep 274 - Why Is My Pair 310x Faster Than std::pair?

结论是让你的简单类型尽可能简单,std::pair过于复杂

项目

https://github.com/Tencent/flare 腾讯出品的一个业务库，嵌入了各种常用客户端/rpc等等
https://github.com/joaquintides/transrangers 更快的range
oceanbase/oceanbase oceanbase又开源了
https://github.com/jk-jeon/dragonbox/tree/1.0.0 高效的float-to-string算法，且合入了fmt库https://github.com/fmtlib/fmt/pull/1882
- 算法细节 https://drive.google.com/file/d/1luHhyQF9zKlM8yJ1nebU0OgVYhfC6CBN/view

本文永久链接

看到这里或许你有建议或者疑问或者指出错误，请留言评论! 多谢! 你的评论非常重要！也可以帮忙点赞收藏转发！多谢支持！

觉得写的不错那就给点吧, 在线乞讨

This site is open source. Improve this page.

C++ 中文周刊 第15期

资讯

编译器信息最新动态推荐关注hellogcc公众号

文章

视频

项目

C++ 中文周刊第15期