数据结构算法相关查缺补漏

刷题单

https://www.lintcode.com/ladder/47/

https://www.lintcode.com/ladder/2/

kuangbin这个太难了。面试不考虑 https://vjudge.net/article/187

https://leetcode-solution-leetcode-pp.gitbook.io/leetcode-solution 这个题解可以看一遍

https://github.com/SharingSource/LogicStack-LeetCode/wiki 这个分类很牛，搜索到这里的同学，看这个wiki就行了。我基本也炒这个

思考

写在纸上

熟悉难度就去研究更难的。suffer
写纸上是个大纲，是更多的点子，在电脑上写有可能局限住，边想边写很容易遗漏

头脑风暴，想法和实现方法

有些时候会卡在思考上，想了半天，一行没写，没法破解成小问题
有时候想法对，但是后续的算法知识你不会，卡住了，或者没有足够的信息往下走了
有时候你后面的解决方法没问题，但想法本身是错误的。换个角度
问题的解决想法很多，可能你得挨个试试，拍个优先级
- 比如求最小值？DP，贪心？最小割？分支界限法
- 简单分析，重新尝试
哪怕是最垃圾的想法，也比没有想法要强，试一试呗

举例/抽象/具象

先用简单例子验证，然后归纳总结通项，然后分析各个元素之间的关系

限制

条件能够判定规模，限制大小

N	复杂度	可能的算法/技巧
10^18	O(log(N))	二分/快速幂/ Cycle Tricks / Big Simulation Steps / Values ReRank
100 000 000	O(N)	贪心？线性算法一般来说
40 000 000	O(N log N)	二分/Pre-processing & Querying/分治
10 000	O(N^2)	DP/贪心/B&B(分支定界)/D&C(分治)
500	O(N^3)	DP/贪心/…
90	O(N^4)	DP/贪心/…
30-50	O(N^5)	Search with pruning/分支定界
40	O(2^(N/2))	Meet in Middle
20	O(2^(N))	回溯/ Generating 2^N Subsets
11	O(N!)	Factorial / Permutations / Combination Algorithm

有些限制也可能是假的/误导人的。注意区别。限制条件非常重要

经典题型

龟兔赛跑
Merge Intervals，区间合并类型
重叠区间，判断交集
Cyclic Sort，循环排序
In-place Reversal of a LinkedList，链表翻转
Tree Breadth First Search，树上的BFS
用队列处理遍历
Tree Depth First Search，树上的DFS
模拟堆栈
Two Heaps，双堆类型 最大最小堆求中位数
优先队列
找一组数中的最大最小中位数
Subsets，子集类型，一般都是使用多重DFS
Modified Binary Search，改造过的二分，旋转数组，找子数组最大值
Top ‘K’ Elements，前K个系列 堆
K-way merge，多路归并
DP
- 0/1背包类型
- Unbounded Knapsack，无限背包
- 斐波那契数列走台阶
- Palindromic Subsequence回文子系列
- Longest Common Substring最长子字符串系列
- Topological Sort (Graph)，拓扑排序类型
hashmap邻接表

双指针

滑动窗口

二分

树的搜索

回溯算法

贪心算法

递归 & 迭代

BFS
DFS

图论

BFS
DFS
多源 BFS
双向 BFS
迭代加深
拓扑排序
最短路
最小生成树
并查集
启发式搜索

动态规划

记忆化搜索
线性 DP
背包 DP
序列 DP
区间 DP
状压 DP
状态机 DP
数位 DP
树形 DP

数据结构

树
二叉树
哈希表
红黑树
链表
栈
单调栈
队列
单调队列
堆
字典树
字符串哈希
后缀数组

区间求和

前缀和
差分
树状数组
线段树
分块
莫队算法

排序

分治

数学

计算几何

容斥原理

多路归并

子串匹配

位运算

最小表示法

博弈论

三分

洗牌算法

二进制枚举

快速幂

矩阵快速幂

找规律

脑筋急转弯

打表

约瑟夫环

高精度

蓄水池抽样

构造 s 原地哈希折半搜索

排序

初级排序

选择排序
- 运行时间和输入无关，并不能保留信息，有记忆信息更高效
插入排序

void insertion_sort(vector<int> &nums, int n) {
    for (int i = 0; i < n; ++i) {
        for (int j = i; j > 0 && nums[j] < nums[j-1]; --j) {
            swap(nums[j], nums[j-1]);
        } 
    }
}

如果有序，更友好
进阶，希尔排序，分组插入排序
- 分组怎么确定？

归并排序

左闭右闭 [l,r]

void merge_sort(vector<int> &nums, int l, int r, vector<int> &temp) {
    if (l + 1>= r) return;
    // divide
    int m = l + (r - l) / 2;
    merge_sort(nums, l, m, temp);
    merge_sort(nums, m, r, temp);
    // conquer
    int p = l, q = m, i = l;
    while (p < m || q < r) {
       if (q >= r || (p < m && nums[p] <= nums[q])) {
           temp[i++] = nums[p++];
       } else {
           temp[i++] = nums[q++];
       }
    }
    for (i = l; i < r; ++i) {
       nums[i] = temp[i];
    }
}

难在原地归并
递归归并

快速排序

左闭右开 [l,r)

void quick_sort(int q[], int l, int r){
    if (l >= r) return;
    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j) {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

大雪菜这个模版还是比较干净利落的 https://www.acwing.com/blog/content/277/

如何选位置？
改进方案
- 小数组用插入排序
- 三取样切分，中位数的选取

优先队列

二叉堆维护

插入
- 加到数组末尾，上浮
删除最大元素
- 最后一个元素放到顶端，下沉

多叉堆

堆排序

查找

基本抽象符号表（dict） put/get/delete/contains

是否需要有序 min/max/range-find
插入和查找能不能都快
- 插入块不考虑查找，链表，插入慢查找快，哈希表？
- 二叉查找树，插入对数查找对数（二分）

散列表

拉链法，也就是每个表项对应一个链表，有冲突就放到链表里
线性探测，放在下一个？？？长键簇会很多很难受

应用

查找表
索引，反向索引
稀疏矩阵哈希表表达

DFS/BFS

最小生成树 MST

加权图权值最小的生成树

Prim/Kruskal
- Prim 贪心 + 优先队列
几个简化
- 权重不同，路径唯一
- 只考虑连通
- 权重可以是负数，意义不一定是距离
树的特点
- 任意两个顶点都会产生一个新的环
- 树删掉一条边就会得到两个独立的树
切分定理
- 给定任意的切分，它的横切边中权重最小的必然是图的最小生成树？？
- 这些算法都是一种贪心算法
  - V个顶点的任意加权连通图中属于最小生成树的边标记成黑色，初始为灰色，找到一种切分，横切边均不为黑色，将它权重最小的横切边标记为黑色，反复，直到标记了V-1条黑色边为止？？

动态规划

求最值的，通常要穷举，聪明的穷举(dp table)
重叠子问题以及最优子结构
- 如果没有最优子结构，改造转换
正确的状态转移方程
- 数学归纳
- dp[i]代表了什么？
  - 最长上升子序列问题，dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度
- 公式条件？
- dp的遍历方向问题
  - 遍历的过程中，所需的状态必须是已经计算出来的。
  - 遍历的终点必须是存储结果的那个位置。

https://github.com/xtaci/algorithms

字符串

vector counts(26, 0);

字符串匹配（KMP）

贪心

策略，局部最优解是什么，扩大化

说实话，很少有应用，更像智力题

双指针

滑动窗口类型
双指针类型
快慢指针类型

可以快慢，也可以左右，也可以滑动，总之是一次遍历收集两种信息

(1) 对于一个序列，用两个指针维护一段区间
(2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操

合并数组，判断链表是否有环(Floyd判定)，链表第K个，链表中间，给你两个字符串，判断包含的最短字符串

双指针有时候只是算法题的一小步，相当于数学压轴提的第一小题，铺垫用，他妈的，算法题为啥这么难

for (int i = 0, j = 0; i < n; i ++ ) {
    while (j < i && check(i, j)) j ++ ;

    // 具体问题的逻辑
}

二分

大雪菜的模版

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r) {
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r) {
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r) {
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

实现lower_bound/upper_bound, 求平方根

int lower_bound(vector<int> &nums, int target) {
    int l = 0, r = nums.size(), mid;
    while (l < r) {
        mid = l + (r - l) / 2;
        if (nums[mid] >= target) { // upper_bound，改下这个条件就行
            r = mid;
        } else {
            l = mid + 1;
        }
    }
    return l; 
}

旋转数组找数组，局部二分

有时候可能target不确定，通过二分来处理target的可能范围，寻找target

位运算

x ^ 0 = x
x & 0 = 0 
x | 0 = x

x ^ 1 = ~x 
x & 1 = x 
x | 1 = 1

x ^ x = 0
x & x = x 
x | x = x

n & (n - 1)  //清空低位, 如果为0，说明是2的次方
n & (-n) // 得到低位

数据结构题

最小栈，匹配括号，桶排序，单调栈，优先队列（堆）

vector<int> heap;
// 获得最大值 
void top() {
    return heap[0];
}
// 插入任意值:把新的数字放在最后一位，然后上浮 void push(int k) {
    heap.push_back(k);
    swim(heap.size() - 1);
}
// 删除最大值:把最后一个数字挪到开头，然后下沉 void pop() {
    heap[0] = heap.back();
    heap.pop_back();
    sink(0);
}
// 上浮
void swim(int pos) {
    while (pos > 1 && heap[pos/2] < heap[pos])) {
       swap(heap[pos/2], heap[pos]);
       pos /= 2;
} }
// 下沉
void sink(int pos) {
    while (2 * pos <= N) {
       int i = 2 * pos;
       if (i < N && heap[i] < heap[i+1]) ++i;
       if (heap[pos] >= heap[i]) break;
       swap(heap[pos], heap[i]);
       pos = i;
} }

hashmap, deque(当滑动窗口用)

前缀和，积分图？

链表

树

二叉查找树

左边小右边大

删除节点

右边大，但是右边的左节点小，要找到右边没有左子节点的左节点，作为被删节点的交换节点
左边一定是小于右边的，所以要确定右边最小的，抬到被删节点的位置就行了
如果删除的是最小节点，那一定是左边的没有左子节点的节点，右子节点直接抬上来就行了，因为左边没了

最坏情况，数不平衡，退化成链表

范围查找也就是中序遍历

平衡查找树

在插入场景下保证二叉查找树的完美平衡难度过大

2-3查找树，插入能尽可能的保持平衡
- 如果插入终点是2节点，就转换成3节点
- 如果终点是3节点
  - 只有一个3节点，该节点编程4节点，4节点可以轻松抽出二叉树子树
    - 父2节点，子3节点，同理，抽出子树，把子树父节点塞到父节点
    - 父3节点，子3节点，同理，抽出子树，把子树父节点塞到父节点，父节点再抽出子树，重复
    - 全是3节点树高 +1
红黑二叉查找树描述2-3树？？
- 替换3节点抽出子树左连接子树要标红有图
- 红连接放平，就是2-3树了
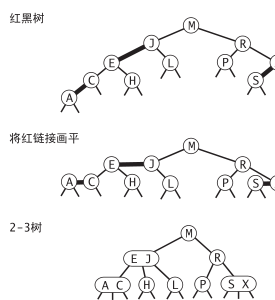
一种等价定义
- 红连接均为左连接
- 没有任何一个节点同时和两条红连接相连
- 完美黑色平衡，任意空连接到根节点的路径上的黑连接相同
旋转就是单纯的改变方向
插入
- 2节点插入
  - 单个2节点插入一个元素就是单个2节点，左边就变红，如果右边变红+旋转最终都是3节点
  - 树底2节点插入，右边，那就旋转（交换位置）
- 双键树插入，3节点插入三种情况，小于/之间/大于
  - 大于，直接放到右边，平衡了，变黑
  - 小于，放到左边，两连红，旋转变黑
  - 之间，放左边右子节点，旋转，在旋转，变黑
删除
红黑树性质
- 高度
- 到任意节点的路径平均长度

###

Trie

class TrieNode {
public:
    TrieNode* childNode[26] = {nullptr};
    bool isVal = false;
};
class Trie {
    TrieNode* root;
public:
    Trie(): root(new TrieNode()) {}
    // 向字典树插入一个词
    void insert(string word) {
       TrieNode* temp = root;
       for (int i = 0; i < word.size(); ++i) {
           if (!temp->childNode[word[i]-’a’]) {
              temp->childNode[word[i]-’a’] = new TrieNode();
            }
           temp = temp->childNode[word[i]-’a’];
       }
       temp->isVal = true;
    }
      // 判断字典树里是否有一个词 
    bool search(string word) {
       TrieNode* temp = root;
       for (int i = 0; i < word.size(); ++i) {
           if (!temp) break;
           temp = temp->childNode[word[i]-’a’];
       }
       return temp? temp->isVal: false;
    }
    // 判断字典树是否有一个以词开始的前缀 
    bool startsWith(string prefix) {
       TrieNode* temp = root;
       for (int i = 0; i < prefix.size(); ++i) {
            if (!temp) break;
            temp = temp->childNode[prefix[i]-’a’];
       }
       return temp;
    }
};

图

无向图 边(edge) 顶点(vertex)

顶点名字不重要，用数字描述方便数组描述

特殊的图 自环 /平行边 含有平行边的叫 多重图 没有平行边/自环的是 简单图

两个顶点通过一条边相连 相邻 这条边 依附于这两个顶点

依附于顶点的边的总数称为顶点的 度数

子图 一幅图的所有变的一个子集以及所依附的顶点构成的图许多问题要识别各种类型的子图

路径 由边顺序链接一系列顶点 u-v-w-x

简单路径 没有重复顶点的路径

环 至少包含一条边，起点终点相同的路径 u-v-w-x-u

简单环 不包含重复顶点和重复边的 环

如果从任意一个顶点都存在一条路径到达另一个顶点，我们称这幅图是 连通图

一幅非连通的图由若干连通部分组成，它们都是极大连通子图

` 无环图` 不包含环的图

树 无环连通图

生成树 连通图的子图，包含所有顶点，且是一棵树

森林 树的集合 生成树森林 生成树的集合

树的定义非常通用便于程序描述

图G 顶点V个

G有V-1条边且不含环
G有V-1条边且连通
G连通，但删除任意一条编都会是它不在联通
G是无环图，添加任意一条边会产生一条换
G中任意一对顶点之间仅存在一条简单路径

图的 密度 已经连接的顶点对栈所有可能被连接的顶点对的比例 稀疏图 被连接的顶点对很少，稠密图 只有很少的抵抗点对之间没有边连接如果一幅图中不同的边的数量在顶点总数的一个很小的常数倍之内就是稀疏的

二分图 能够将所所有节点分成两部分的图

图的表达方式

要求，空间，快
- 邻接矩阵 V*V矩阵空间太大
  - 平行边无法描述
- 边的数组查相邻不够快
- 邻接表数组顶点为索引的数组，数组内是和该顶点相邻的列表
  - 空间 V+E
遍历
- DFS 其实也是dp数组方法的一种递归要用堆栈
- 连通性判定
寻找路径，路径最短判定？
- BFS
连通分量？
间隔的度数？

有向图

有向图取反

有向图的可达性

mark-sweep gc
有向图寻路
- 单点有向路径
- 单点最短有向路径

环/有向无环图(DAG)/有向图中的环

有向环检测,有向无环图就是不含有有向环的有向图
- dfs
有向图中的强连通性
- 构成有向环
- 自反/对称/传递

https://github.com/ouuan/Tree-Generator

https://csacademy.com/app/graph_editor/

画图工具

一些模版

https://github.com/Strive-for-excellence/ACM-template

https://github.com/atcoder/ac-library

https://github.com/kth-competitive-programming/

https://github.com/hanzohasashi33/Competetive_programming

博弈问题 https://zhuanlan.zhihu.com/p/50787280

https://hrbust-acm-team.gitbooks.io/acm-book/content/ 面试不用搞这么难